Sandwich Panels: Derivation of calculations

Derivation of calculations

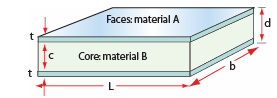
A sandwich panel epitomizes the concept of a hybrid. It combines two materials in a specified geometry and scale, configured such that one forms the faces, the other the core, to give a structure of high bending stiffness and strength at low weight (see Figure 1). The separation of the faces by the core increases the moment of inertia of the section, I, and its section modulus, Z, producing a structure that resists bending and buckling loads well. Sandwich panels are used where weight-saving is critical: in aircraft, trains, trucks and cars; in portable structures; and in sports equipment. Nature, too, makes use of sandwich designs: sections through the human skull, the wing of a bird, and the stalk and leaves of many plants show a low-density foam-like core separating solid faces (see the texts in Further reading).

Figure 1. The sandwich: The face thickness is t, the core thickness is c and the panel thickness is d

The faces, each of thickness t, carry most of the load, so they must be stiff and strong; and they form the exterior surfaces of the panel so they must also tolerate the environment in which it operates. The core, of thickness c, occupies most of the volume; it must be light, and stiff and strong enough to carry the shear stresses necessary to make the whole panel behave as a load bearing unit (if the core is much thicker than the faces these stresses are small).

Top

A sandwich as a "material"

So far we have spoken of the sandwich as a structure: faces of material A supported on a core of material B, each with its own density, modulus and strength. But we can also think of it as a material with its own set of properties, and this is useful because it allows comparison with more conventional materials. To do this we calculate equivalent material properties for the sandwich, identifying them, as with composites, by a tilde (e.g. 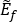, ). The quantities and can be plotted on the modulus-density chart, allowing a direct comparison with all the other materials on the chart. All the constructions using material indices apply unchanged. We base the analysis on the symmetric sandwich with the dimensions defined in Figure 1. The symbols that appear in this section are defined here: symbols.

Physical properties

Density

The equivalent density of the sandwich (its mass divided by its volume) is

(1)

Here f is the volume fraction occupied by the faces: f = 2t / d.

Mechanical properties

Young's modulus

Sandwich panels are designed to be stiff and strong in bending. In thinking of the panel as a "material" we must therefore distinguish the in-plane modulus and strength from those in bending. The effective in-plane modulus, , and strength, , are given, to an adequate approximation, by the rule of mixtures.

In-plane and through-thickness moduli are simply the arithmetic and harmonic means of the components.

(in-plane)

(2)

(through-thickness)

(3)

Flexural modulus

The flexural properties are quite different. The flexural compliance (the reciprocal of the stiffness) has two contributions, one from the bending of the panel as a whole, the other from the shear of the core (see Figure 2). The contributions from both are added together.

Figure 2. Sandwich panel flexural stiffness. There are contributions from bending and from core shear.

The bending stiffness is

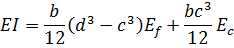
The shear stiffness is

Summing deflections gives:

Here the dimensions d, c, t and L are identified in Figure 1, E_f is Young's modulus of the face-sheets and G_c is the shear modulus of the core. The load configuration determines the constant values (B₁, B₂, B₃ and B₄) as summarized in Table 1. Comparison with for the "equivalent" material gives

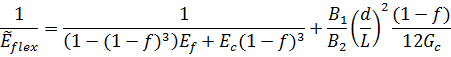Note that, except for the bending-to-shear balancing term ( d / L ) ² the equivalent property is scale-independent (as a material property should be); the only variable is the relative thickness of faces and core, f. The bending stiffness (EI) is recovered by forming the , where is the second moment of a homogeneous panel ().

Table 1. Constants to describe modes of loading

Support and load conditions		Loading constants
		B1	B2	B3	B4
	Built-in ends, central load	192	4	8	2
	Built-in ends, uniformly distributed load	384	8	12	2
	Cantilever, central load	3	1	1	1
	Cantilever, uniformly distributed load	8	2	2	1
	Simply supported, central load	48	4	4	2
	Simply supported, uniformly distributed load	384/5	8	8	2

Yield strength (in-plane and through-thickness)

We calculate the in-plane yield strength using an equal strain assumption. It is assumed that the panel fails when either the core or the face-sheets experience a strain greater than their critical failure strain:

The through-thickness yield strength is the lesser of those of the faces and core:

Figure 3. Failure modes of sandwich panels in flexure

Flexural strength

Sandwich panels can fail in flexure in many different ways (see Figure 3). The failure mechanisms compete, meaning that the one that happens at the lowest load dominates. We calculate an equivalent strength for each mode, then seek the lowest.

Face yield. The fully plastic moment of the sandwich is:

The equivalent flexural strength when face yielding is the dominant failure mode is then:

which, again, is independent of scale.

Face buckling. In flexure, one face of the sandwich is in compression. If it buckles, the sandwich fails. The face-stress at which this happens is:

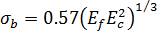
The failure moment M_f is then well approximated by:

Equating this to:

gives

Core shear. Failure by core shear occurs at the load:

Here the first term results from shear in the core (shear strength τ_y,c), the second from the formation of plastic hinges in the faces. Equating to:

gives the equivalent strength when failure is by shear:

(The load configuration determines the constant values B₃ and B₄, as summarized in Table 1.) When the core material is roughly isotropic (as foams are), τ_y,c can be replaced by σ_c,c / 2. When it is not (an example is that of a honeycomb core), τ_y,c must be retained.

Core bending. In the extreme case that face-sheets have very low strength, or that the face-sheet thickness is set to zero, the "sandwich" still exhibits the bending strength of the core itself:

The flexural strength, 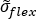, is set equal to:

Indentation has to be treated separately as a constraint on the face-sheet thickness. The indentation pressure is:

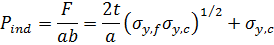
where a = the length of the indenter, b = width of the panel, t = thickness of face-sheet and F = force applied. Further details can be found on pages 117-118 of "Metal foams A Design Guide" by Ashby et al 2000.

Thermal properties

Specific heat capacity

The volumetric specific heat, , follows a rule of mixtures:

Thermal conductivity

The in-plane conductivity is just the sum of the contributions from core and faces:

The through-thickness conductivity, , is given by the harmonic mean:

Thermal expansion coefficient

Thermal expansion in-plane is complicated by the fact that faces and core have different expansion coefficients, but being bonded together, they are forced to suffer the same strain. This constraint leads to an in-plane expansion coefficient of:

The through-thickness coefficient is simpler; it is given by the weighted mean

Thermal diffusivity (through-thickness)

The through-thickness thermal diffusivity is not a single-valued quantity, but depends on time. At short times, heat does not penetrate the core and the diffusivity is that of the face, but at longer times, the diffusivity tends to the value given by the ratio .

Electrical properties

Electrical resistivity (through-thickness)

Dielectric constant

The dielectric constant of a sandwich, as with composites, is given by a rule of mixtures:

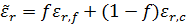
provided both ε_r,f and ε_r,c exist. If either one does not exist, leave blank.

Dielectric loss tangent

provided both D_ε,f and D_ε,c exist. If either one does not exist, leave blank.

Primary material production: energy, CO2 footprint and water

The embodied energy is calculated as a simple rule of mixtures:

And as such only calculates the embodied energy of the constituent materials. It does not include the energy involved in processing or adhesives.

The same is true of the CO2 footprint. Only the relative proportions of the constituent materials are taken into account so it too is described by a rule of mixtures:

Top

Further reading

The books by Allen (1969), Zenkert (1995), Gibson and Ashby (1997), and Ashby et al (2000) give introductions to the design of sandwich panels for engineering applications. That by Gibson et al (2010) does the same for their use in nature.

Copyright © 2020, Granta Design, Cambridge, UK