Cellular Structures: Derivation of calculations
Derivation of calculations
Cellular structures - foams, lattices and honeycombs - are hybrids of a solid and a gas. The properties of the gas might at first sight seem irrelevant, but this is not so. The thermal conductivity of low-density foams of the sort used for insulation is determined by the conductivity of the gas contained in its pores; and the dielectric properties, and even the compressibility, can depend on the gas properties.
There are three distinct species of cellular solid. The first, typified by foams, are bending-dominated structures; the second, typified by triangulated lattice structures, are stretch-dominated - a distinction explained more fully below. The third are honeycombs which exhibit anisotropy (the in-plane properties are different to the through-thickness properties). The in-plane mechanical properties are bending-dominated while the through-thickness ones are stretch-dominated.
Foams are cellular solids made by expanding polymers, metals, ceramics or glasses with a foaming agent - a generic term for one of many ways of introducing gas, much as yeast does in bread-making. Figure 1 shows an idealized cell of a low-density open-cell foam. It consists of solid cell walls or edges surrounding a void space containing a gas or fluid. Foams have the characteristic that, when loaded, the cell walls bend. Lattice structures (Figure 2) are configured to suppress bending, so the cell edges have to stretch instead.
Figure 1. A cell in a low density foam. When the foam is loaded, the cell edges bend, giving a low-modulus structure.
Figure 2. A triangulated lattice structure and its unit cell. The cell edges stretch when the structure is loaded, making it stiffer and stronger than a foam of the same density.
Honeycombs have direction dependent properties (anisotropic) depending on the loading configuration. Furthermore, expanded honeycombs, which have 1/3 of the cell walls with double thickness, have an additional degree of anisotropy in the plane with different properties in the 'L' and 'W' directions (see Figure 3).
Figure 3. The difference between extruded and expanded honeycombs
Physical properties
Density
Open-cell foams and triangulated lattices
Cellular solids are characterized by their relative density, which for the structure shown here (with t << L) is
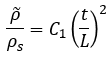
where 
is the density of the foam, ρs is the density of the solid of which it is made, L is the cell size, t is the thickness of the cell edges, and C1 is a constant, approximately equal to 1.
Closed-cell foams
For closed-cell foams, the thickness of the cell faces needs to be taken into account also so the relative density is:
Where te is the cell edge thickness, tf is the face thickness and L is the cell size. In order to calculate properties in terms of the parameter φ (the proportion of bulk material in the cell edges) then the following substitutions can be made:
Honeycombs
For regular (hexagonal with all cell edges the same length, thickness and at the same angle) extruded honeycombs the relative density is given by:
Again where t is the cell wall thickness and assuming t<<L where L is the cell edge length.
For an expanded honeycomb where 1/3 of the cell walls are double thickness (but it is still a regular hexagonal structure) the relative density is given by:
Mechanical properties
The compressive stress-strain curve of a cellular solid looks like Figure 4. The material is linear elastic, with modulus 
up to its elastic limit, at which point the cell edges yield, buckle or fracture. The foam continues to collapse at a nearly constant stress (the "plateau stress", 
) until opposite sides of the cells impinge (the "densification strain" 
), when the stress rises rapidly. The mechanical properties are calculated in the ways developed below (details in the texts in Further reading).
Figure 4. The modulus is determined by cell edge bending or stretching. The plateau stress is determined by buckling, plastic bending or fracturing of the cell walls.
Elastic moduli of bending-dominated open-cell foams
A remote compressive stress σ exerts a force 
on the cell edges, causing them to bend and leading to a bending deflection δ, as shown in Figure 1. For the open-celled structure shown in the figure, the bending deflection scales as
where Es is the modulus of the solid of which the foam is made and 
is the second moment of area of the cell edge of square cross section, t × t. The compressive strain suffered by the cell as a whole is then 
. Assembling these results gives the modulus 
of the foam as
 |
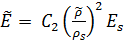(bending-dominated behavior) |
Since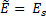 
when 
, we expect the constant of proportionality C2 to be close to unity - a speculation confirmed by experiment. Numerical simulation gives C2 = 0.7, the value used in the Synthesizer. The quadratic dependence means that a small decrease in relative density causes a large drop in modulus. When the cells are equiaxed in shape, the foam properties are isotropic with shear modulus, bulk modulus and Poisson's ratio via
Elastic moduli of bending-dominated closed-cell foams
There are three main contributions to the elastic modulus of a closed-cell foam. The first is the contribution from cell edge bending. There is also a very small contribution from cell face bending too but as this is always small we shall ignore it. The contribution from cell edge bending is very similar to that from open-celled foams (but multiplied by a different constant and involving the parameter φ2):
The second contribution is from the compression of the cell fluid. The contribution to the modulus is:
Where p0 is the internal pressure in the cells. This contribution is very small and can generally be ignored if p0 is equal to atmospheric pressure. This term only really has to be considered if p0 is high or a different fluid (such as a liquid) is used instead of air. For this model it is assumed that the fluid inside the cells is air.
The third contribution to the modulus comes from the membrane stresses in the cell faces and adds a term with the form:
Summing all the contributions (and using the limits where 
to reason that 
) gives the total equivalent modulus as:
Elastic moduli of stretch-dominated lattices
The structure shown in Figure 2 is fully triangulated. This means that the cell edges must stretch when the structure is loaded elastically. On average, one-third of its edges carry tension when the structure is loaded in simple tension, regardless of the loading direction. Thus
 |
(stretch-dominated behavior) |
The modulus is linear, not quadratic, in density, giving a structure that is stiffer than a foam of the same density. The structure of Figure 4 is almost isotropic, so we again approximate the shear modulus, bulk modulus and Poisson's ratio by:
Elastic moduli of extruded honeycombs
When an in-plane stress is applied to a regular uniform honeycomb the wall deflection, δ, is given by:
Where 
and 
is the second moment of inertia of the cell wall. The strain is then:
The modulus 
is then:
Elastic moduli of expanded honeycombs
Adapting the equations used for extruded honeycombs (which are valid as it is the walls with thickness t that determine the elastic response) but using the different ratio between t/L and relative density gives:
Strength of bending-dominated open-cell foams (yield, flexural and compressive strength)
When the structure of Figure 1 is loaded beyond the elastic limit, its cell walls may yield, buckle elastically or fracture as shown in Figure 5. Consider yielding first (Figure 5a). Cell edges yield when the force exerted on them exceeds their fully plastic moment:
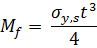
where σy,s is the yield strength of the solid of which the foam is made. This moment is related to the remote stress by 
. Assembling these results gives the compressive failure strength when yield dominates, 
 |
(yield of foams) |
where the constant of proportionality, 0.3, has been established both by experiment and by numerical computation.
Figure 5. Collapse of foams. (a) When a foam made of a plastic materials is loaded beyond its elastic limit, the cell edges bend plastically. (b) An elastomeric foam, by contrast, collapses by the elastic buckling of its cell edges. (c) A brittle foam collapses by the successive fracturing of cell edges.
Elastomeric foams collapse not by yielding but by elastic bucking; brittle foams by cell-wall fracture (Figures 5 (b) and (c)). As with plastic collapse, simple scaling laws describe this behavior well. Collapse by buckling occurs when the stress exceeds
 |
(buckling of foams) |
We identify the compressive strength with the lesser of equations for . We further set the yield strength 
and the flexural strength 
equal to .
Strength of bending-dominated closed-cell foams
As with modulus there is more than one contribution to the yield strength on closed-cell foams. There is a contribution from the internal gas pressure, p0, though this is insignificant if the internal pressure is close to atmospheric pressure so we will ignore it. The significant contributions are from the yield of the cell edges and the membrane stresses in the cell faces. The contribution from edge yield is:
The contribution from membrane stresses takes the form:
So the overall compressive yield strength is then the sum of these contributions:
However, if an elastomeric foam is used then the foam may fail by elastic buckling with the failure stress given by the density corrected equation:
As with open-cell foams we identify the least out of 
and 
as the compressive, yield and flexural strength.
Strength of stretch-dominated lattices
Collapse occurs when the cell edges yield, giving the collapse stress
 |
(yield of lattices) |
This is an upper bound since it assumes that the struts yield in tension or compression when the structure is loaded. If the struts are slender, they may buckle before they yield. They do so at the stress
 |
(buckling of lattices) |
We identify the compressive strength with the lesser of and . We further identify the yield strength and the flexural strength with .
Strength of extruded honeycombs
The through-thickness values are returned for compressive and yield strength while the flexural strength is returned for bending about an axis in-plane. In compression the two modes of failure are plastic collapse of the cell walls or the elastic buckling of them if they are thin. The plastic yield of them is given by:
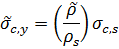
The elastic buckling stress for an extruded honeycomb in compression is:
The analysis to return this value can be found on pages 152–153 of Gibson & Ashby (1997).
The compressive strength is then identified as the lesser of these two. The yield strength is given by the equivalent expression for but in tension (and therefore the equation for elastic buckling is not applicable):
The flexural strength of the honeycomb in bending about an in-plane axis will be the lesser of the two failure modes, plastic collapse or elastic buckling. The equation for plastic collapse is found by equating the work done by a force during a plastic rotation of four plastic hinges to the plastic work done at the hinges (details to be found on pages 110 & 111 of Gibson & Ashby (1997)). The other mode of failure in flexure is elastic buckling (details to be found on pages 106–110 of Gibson & Ashby (1997)). The flexural strength is then defined as:
Strength of expanded honeycombs
As with extruded honeycombs the through-thickness values are returned for the compressive and yield strengths, while for flexural strength the failure stress for bending about an in-plane axis is returned. In compression the simple plastic yield of the cell walls is given by:
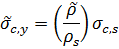
The elastic buckling in through-thickness compression is given by:
This equation is found in the appendix on page 171 of Gibson & Ashby (1997). The constant is calculated by evaluating the geometric terms for a regular hexagonal honeycomb.
The compressive strength is then identified as the lesser of these two failure modes.
As with the extruded honeycombs the tensile strength is identified as:
As elastic buckling is not applicable for through-thickness tension.
The flexural strength will again be the lesser of the two failure modes, plastic collapse and elastic buckling in-plane:
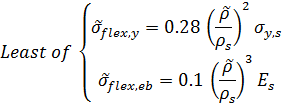
These equations are also taken from the appendix on page 171 of Gibson & Ashby (1997).
Fracture toughness of foams
Foams that contain crack-like flaws that are long compared to the cell size, l, fail by fast fracture, meaning that the crack propagates unstably if the stress intensity factor exceeds the critical value 
, which is:
Here a is the intrinsic flaw size of the material, in the cell edges, 
is its fracture toughness. Typically l / a = 10, the default value used in the Synthesizer Tool.
This behavior is not confined to open-cell foams. Most closed-cell foams also follow these scaling laws, at first sight an unexpected result because the cell faces must carry membrane stresses when the foam is loaded, and these should lead to a linear dependence of both stiffness and strength on relative density. The explanation lies in the fact that the cell faces are very thin; they buckle or rupture at stresses so low that their contribution to stiffness and strength is small, leaving the cell edges to carry most of the load.
Fracture toughness of stretch-dominated lattices
Lattices that contain crack-like flaws that are long compared to the cell size l fail by fast fracture, meaning that the crack propagates unstably if the stress intensity factor exceeds the critical value , which is:
l / a is the ratio of the cell size of the foam to the flaw size in the material. A default value l / a = 10 is used in the Synthesizer Tool.
Fracture toughness of honeycombs
Honeycomb walls that contain crack-like flaws that are long compared to the cell size, l, fail by fast fracture, meaning that the crack propagates unstably, if the stress intensity factor exceeds the critical value , which is:
l / a is the ratio of the cell size of the foam to the flaw size in the material. A default value l / a = 10 is used in the Synthesizer Tool.
Thermal properties
Specific heat and thermal expansion
The specific heat 
(units: J/kg.K) of foams and lattices and the expansion coefficient 
(units K-1) are the same as those of the solid of which they are made. This result holds for closed cell foams made from a rigid material, however, if an elastomeric material is used then the expansion of the internal gas may make the coefficient of thermal expansion appear larger.
Thermal conductivity
Foams and lattices
The cells in most foam and lattice structures are sufficiently small that convection of the gas within them is completely suppressed. The thermal conductivity of the foam or lattice is then the sum of that conducted thought the cell walls and that through the still air (or other gas) they contain. To an adequate approximation
where λs is the conductivity of the solid and λg that of the gas (for dry air it is 0.025 W/m.K). The term associated with the gas is important: blowing agents for foams intended for thermal insulation are chosen to have a low value of λg. One of the assumptions used is that the gas contained in the cells is air.
Honeycombs
The model returns the through-thickness thermal conductivity which is just the weighted arithmetic mean of the solid and gas fractions:
Again the gas contained in the cells is assumed to be air.
Electrical properties
Resistivity
Foams and lattices
The electrical resistivity, 
of a foam or lattice is given by
Honeycombs
As with thermal conductivity the through-thickness value is returned, which for a honeycomb is:
Dielectric properties
Insulating foams, lattice structures or honeycombs are attractive for their low dielectric constant, 
, falling towards 1 (the value for air or vacuum) as the relative density decreases:
where εr,s is the dielectric constant of the solid of which the foam is made.
The dielectric loss tangent is independent of foam density and is equal to that of the solid of which the foam is made.
Sources
Principal sources for the derivation of these models are: Gibson and Ashby (1997), Deshpande et al (2001), Ashby et al (2000), Ashby (2006).
Copyright © 2020, Granta Design, Cambridge, UK