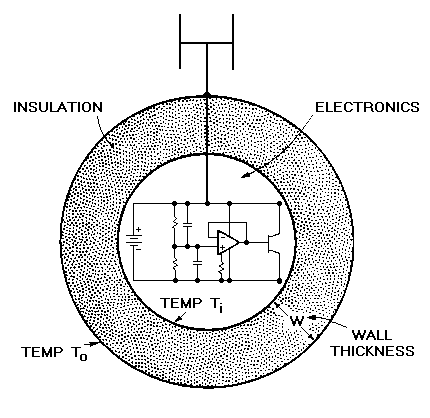
Each member of the crew of a military aircraft carries, for emergencies, a radio beacon. If forced to eject, the crew-member could find himself in trying circumstances — in water at 4°C, for example (much of the earth's surface is ocean with a mean temperature of 4°C). The beacon guides friendly rescue services to the crew member, minimizing exposure time.
But microelectronic (like human) metabolisms are upset by low temperatures. In the case of the beacon, the transmission frequency starts to drift. The design specification for the egg-shaped package containing the electronics (Figure 20.1) requires that, when the temperature of the outer surface is changed by 20°C, the temperature of the inner surface should not change significantly for one hour. To keep the device small, the wall thickness is limited to a thickness W of 20 mm. What is the best material for the package? A dewar system is ruled out — it is too fragile.

Figure 20.1 An electronic beacon. The insulation should prevent the temperature of the electronics falling for at least one hour.
A foam of some sort, you might think. But here is a case in which intuition leads you astray. So let us formulate the design requirements and do the job from first principles. Table 20.1 lists the design requirements.
|
FUNCTION |
Thermal insulation |
|
OBJECTIVE |
Maximize time t before temperature falls, 1°C |
|
CONSTRAINTS |
Wall thickness = W |
Table 20.1 The design requirements
We model the container as a wall of thickness W, and thermal conductivity λ. Once a steady-state has been established, the heat flux J through the wall is
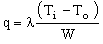 , , |
(M20.1) |
where To is the temperature of the outer surface and Ti that of the inner one (Figure 20.1). This heat flux can be minimized by choosing a wall material with the lowest possible value of
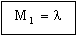 . . |
(M20.2) |
But we have answered the wrong question. The design brief was not to minimize the heat flux, but the time before the temperature of the inner wall changed appreciably (1°C). When the surface temperature of a body is suddenly changed, a temperature wave, so to speak, propagates inwards. The distance X it penetrates in time t is approximately X = √(2at) Here a is the thermal diffusivity, defined by
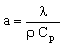 , , |
(M20.3) |
where ρ is the density and Cp is the specific heat. Equating distance X to the wall thickness gives
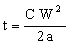 , , |
(M20.4) |
where C is a constant with a value close to 1. The time is maximized by choosing the smallest value of the thermal diffusivity:
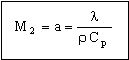 . . |
(M20.5) |
Selection for both the steady-state and the transient problem is made possible by a chart in which thermal conductivity is plotted against thermal diffusivity. Figure 20.2 shows such a chart, constructed using the Generic record subset. One axis is the thermal conductivity, λ ; the other is the compound property λ/ρCp.
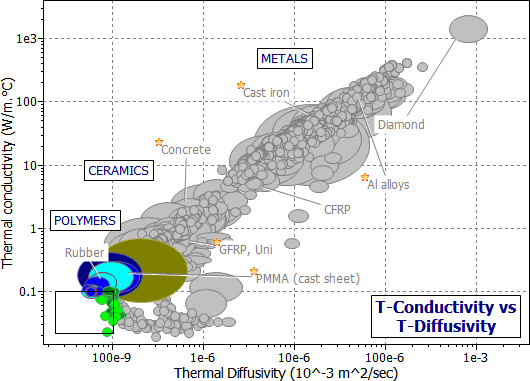
Figure 20.2 A chart showing thermal conductivity λ plotted against thermal diffusivity, a, constructed with the Generic record subset. Materials for long-term insulation should have low λ ; those for short-term insulation should have low a.
The figure shows that polymer foams have low conductivities, and thus are good for insulation at steady-state (as in wall insulation). But their thermal diffusivities are not particularly low; because they have so little mass, and thus low heat capacity Cp. The materials with low diffusivity for heat are solid polymers and — particularly — solid elastomers.
And now we need more detail. It is to be found in the Polymers record subset (Figure 20.3). A package made of solid elastomer such as butyl rubber (BR), polychloroprene (CR) or chlorosulfinated polyethylene (CSM) would give the beacon up to a factor 10 longer transmission-life than one of the same thickness made of (say) a low density polystyrene foam (e.g. PS 0.05). This difference is brought out in Figure 20.4, in which thermal diffusivity is plotted as a bar-chart, with the columns showing the material classes of the Polymers record subset. Elastomers clearly offer the best performance for short-term thermal insulation. The selection is summarized in Table 20.2. The reader can confirm, using equation (M20.4), that 22 mm of a solid elastomer (a = 7 x 10-8 m2/s, read from the figure) will allow a time interval of 1 hour after an external temperature change before the internal temperature shifts significantly.
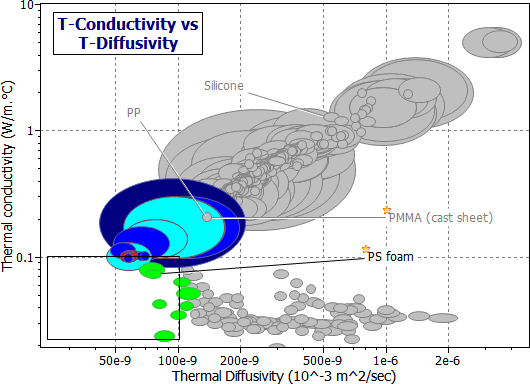
Figure 20.3 The same chart as Figure 20.2, constructed using the Polymers record subset. Materials for both short and long-term insulation are identified.
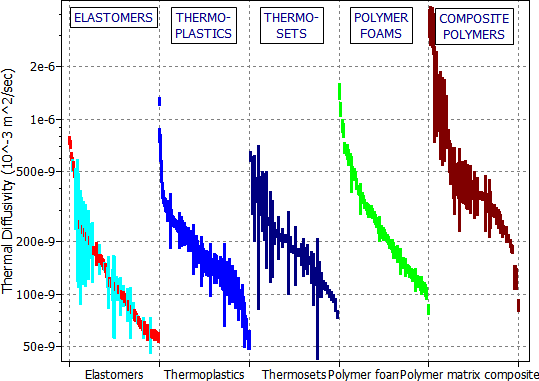
Figure 20.4 A bar-chart of thermal diffusivity, a, for the five classes of materials in the Polymers record subset. The chart shows the superiority of elastomers for short-term insulation.
|
MATERIAL |
COMMENT |
|
Elastomers: Butyl rubber (BR), Polychloroprene (CR), and Chlorosulfinated polyethelene (CSM) are examples |
Best choice for short-term insulation |
|
Commodity polymers: |
Cheaper than elastomers, but somewhat less good for short-term insulation |
|
Polymer foams |
Much less good than elastomers for short-term insulation; best choice for long-term insulation at steady state. |
Table 20.2 Materials for thermal insulation
One can do better than this. The trick is to exploit other ways of absorbing heat. If a liquid — a low-melting wax, for instance — can be found that solidifies at a temperature equal to the minimum desired operating temperature of the transmitter Ti, it can be used as a 'latent-heat sink'. Channels in the package are filled with the liquid. The inner temperature can only fall below the desired operating temperature when all the liquid has solidified. The latent heat of solidification must be supplied to do this, giving the package a large (apparent) specific heat, and thus an exceptionally low diffusivity for heat at the temperature Ti. The same idea is, used in reverse in 'freezer packs' which solidify when placed in the freezer compartment of a refrigerator and remain cold (by melting, at 4°C) when packed around warm beer cans in a portable cooler.
Holman, JP 'Heat Transfer', 5th Edition, (1981), McGraw-Hill, NY, USA.