.jpg)
Microchips only consume milliwatts of power, but their dimensions are minuscule. The power is low but the power-density is high. As chips shrink and processing speeds grow, heating becomes a problem. The Pentium chip of today's computers already gets quite hot. Multiple-chip modules (MCMs) pack as many as 130 chips on to a single substrate, make the problem worse. Heating is kept under control by attaching the chip to a heat sink (Figure 28-1), taking pains to ensure good thermal contact between the chip and the sink. The heat sink now becomes a critical component, limiting further development of the electronics. How can its performance be maximized?
The purpose of a heat sink is to drain heat away from the chip as fast as possible. But it must do more than that. It must, for example, have a thermal expansion coefficient which is close to that of the chip itself, otherwise thermal stress caused by relative expansion will damage the electronics. Weight is also a consideration: for aerospace applications the sink should be as light as possible. And cost, although not a primary consideration, cannot be overlooked entirely. Table 28-1 summarizes the requirements.
.jpg)
Figure 28-1. A heat sink. The heat flows from the chip to the external surface of the heat sink driven by the temperature gradient ΔT/X
FUNCTION |
Heat sink |
OBJECTIVE |
Maximum heat flux per unit weight |
CONSTRAINTS |
(a) Limit on expansion relative to silicon |
(b) Cost could be a consideration |
Table 28-1. The design requirements
We assume that the chip operates continuously and that the finned face of the heat sink is cooled by a fan or by water-cooling which keeps its temperature at To. Then the power which is drained from the chip is, to an adequate approximation,
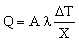 |
(M28.1) |
where A is the contact area between chip and heat sink, λ is the thermal conductivity of the sink, ΔT the temperature difference across the sink, and X the sink thickness. Values of Q/A can be as high as 200 kW/m2. The area of the sink is itself proportional to A — a big chip obviously needs a big sink; let us write it as CA. So the mass of the sink is
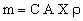 |
where ρ is the density of the material of which it is made. The power drained per unit weight is thus
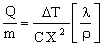 |
(M28.2) |
This is the objective function.
The temperature difference ΔT is limited by thermal expansion — too high a temperature will cause differential strain between chip and sink which will damage the chip. The expansion difference is
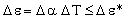 |
where Δα is the difference in coefficient of thermal expansion between sink and chip. Δε must be kept below the damaging value Δε*. Using this constraint to eliminate ΔT in equation (M28.2) gives
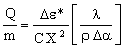 |
(M28.3) |
Performance is maximized by maximizing the group of material properties
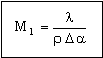 |
(M28.4) |
This result can be used to select materials in several ways. The most convenient is to seek materials with high values of λ/ρ while imposing a restriction on the expansion difference Δα :
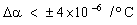 |
(M28.5) |
To do this we need a chart with M1 = λ/ρ as one axis and M2 = α as the other (Figures M28.2 and M28.3). The limits on α are drawn on the chart and the subset of materials which lie between these brackets and which maximize M1 are read off. The first figure uses the 'All bulk materials' record subset; in the second, a custom subset of the 'light alloys' has been chosen (aluminum, beryllium, magnesium, titanium alloys and aluminum matrix composites). Table 28-2 lists the results.

Figure 28-2. A chart of conductivity per unit weight, λ/ρ , against expansion coefficient α , using the 'All bulk materials' record subset, showing the index M1

Figure 28-3. Data from the 'light alloys' custom subset, shown on the same axes as those of Figure 28.2
Some pretty exotic materials have been developed for heat sinks. Most are composites, often of two metals, one to give good conductivity, the other to limit thermal expansion. Blends of tungsten (W) and copper, of molybdenum (Mo) and copper, or copper-coated Invar are good, but all of them are heavy. Copper reinforced with high-conductivity carbon fibers is lighter, but very expensive; aluminum reinforced with beryllium oxide is also light but potentially toxic. At present, aluminum reinforced with particulate silicon carbide looks like the best compromise, most nearly meeting the design requirements.
MATERIAL |
COMMENT |
Metal matrix composites |
Al – 70% SiC out-performs all competing materials |
Copper, Silver, Gold |
Conduct well, but expand too much and are heavy |
Beryllium alloys |
Good conduction, tolerable expansion, very light |
Light alloys: Aluminum, and Magnesium |
Conduct well and are light, but expand too much |
Tungsten, Molybdenum |
Good match of expansion coefficient to silicon, but conduct less well and are very heavy |
Titanium alloys |
Expansion acceptable, but poor thermal conductor |
Possible developments |
Beryllium – silicon carbide composites? |
Table 28-2. Materials for heat sinks
Zweben, C, Journal of Metals, 44 (7), July 1992, p. 15–23.
Premkumar, MK, Hung, WH Jr., and Sawtell, RR, Journal of Metals, 44 (7), July 1992, p. 24–28.