Materials For Table Legs

• Introduction
• The Model
• The Selection
• Postscript
• Further reading
• Related case studies

Introduction

Luigi Tavolino, furniture designer, conceives of a light-weight table of daring simplicity: a flat sheet of toughened glass supported on slender, unbraced, cylindrical legs (Figure 4-1). The legs must be solid (to make them thin) and as light as possible (to make the table easier to move). They must support the table top and whatever is placed upon it without buckling. What materials could one recommend?

Figure 4-1. A light-weight table with slender cylindrical legs. Lightness and slenderness are independent design objectives, both constrained by the requirement that the legs must not buckle when the table is loaded.

Table 4-1. The design requirements

The Model

Table 4-1 lists the design brief. This is a problem with two design objectives: weight is to be minimized, and slenderness maximized. There is one constraint: resistance to buckling. Consider minimizing weight first.

A leg is a slender column of material with density ρ and modulus E. Its length, l, and the maximum load, P, it must carry are fixed by the design. The radius r of the leg is a free variable. We wish to minimize the mass m of the leg, given by the objective function

(M4.1)

subject to the constraint that it supports a load P without buckling. The elastic load P_crit of a column of length l and radius r is

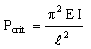(M4.2)

where I = π r⁴/4 is the second moment of area of the column. The load P must not exceed P_crit. Solving for the free variable, r, and substituting it into equation M4.1 gives

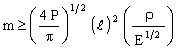(M4.3)

The material properties are grouped together in the last set of brackets. The mass is minimized by selecting the subset of materials with the greatest value of the performance index

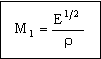(M4.4)

Now consider slenderness. Inverting equation (M4.2) gives an equation for the thinnest leg which will not buckle under the design load P:

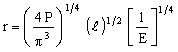(M4.5)

The thinnest leg is that made of the material with the largest value of the index

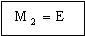(M4.6)

There is another constraint, that of shock-resistance; the legs must not fracture if accidentally struck. Shock-resistance requires an adequate value of the toughness, G_c = K_1c² / E , not merely fracture toughness, K_1c . A useful rule-of-thumb for this is to choose materials with a toughness, G_c, such that

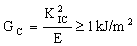And cost, says Snr. Tavolino, is of "interest".

The Selection

We seek first the subset of materials which have high values of E^1/2/ρ and E. Figure 4-2 shows the appropriate chart: Young's modulus, E, plotted against density, ρ. A selection line is positioned at M₁ = 0.0048 GPa^1/2/(kg/m³). Materials above this line have high values of M₁. They include woods (the traditional material for table legs), composites (particularly CFRP) and certain special engineering ceramics. Polymers are out: they are not stiff enough; metals are too heavy.

The choice is further narrowed by the requirement that, for slenderness, E must be large. A horizontal line on the chart at M₂ = 100 GPa eliminates woods and GFRP. If the legs must be slender, then the short list is reduced to CFRP and ceramics; if light (but not so slender) then wood is good.

Figure 4-2(a). The E-ρ chart. The diagonal line shows the index M₁ = 0.0048 GPa^1/2/(kg/m³); Wood is a good choice; so is a composite such as CFRP. Ceramics meet the stated design goals, but are brittle.

Figure 4-2(b). The E-ρ chart. The horizontal line shows the M₂ = 100 GPa buckling constraint.

Figure 4-3. The G_c - C_m chart. The box contains materials with G_c  > 1 kJ/m² and C_m < 100 USD/kg. Woods, and the composite CFRP satisfy both these criteria and those defined by M₁ and M₂

Table legs are exposed to abuse — they get knocked and kicked. Common sense suggests that an additional constraint is needed, that of adequate toughness. This is achieved by creating a chart with toughness, G_c, as one axis. (Do this in Granta EduPack by generating the 'user-defined' property K_1c² / E , and naming it 'Toughness'.) In Figure 4-3 the toughness is plotted against cost/kg, C_m. Putting a lower limit of

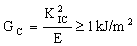on G_C, but no limit on cost, identifies CFRP as the best choice for legs. The cost of CFRP may cause Snr. Tavolino to reconsider his design, but that is another matter; he did not mention a limit on cost in his original specification. Had he done so, a cost-limit could be added on Figure 4-3 by moving the right-hand edge of the box, but requiring a relaxation of the stringent conditions on M₁ and M₂. A severe cost-limit leaves woods, especially spruce, palm and pine as the prime candidates.

It is a good idea to lay out the results as a table, showing not only the materials which are best, but those which are second-best. When other factors are considered they may become the best choice. Table 4-2 shows one way of doing it.

Table 4-2. Materials for table legs

Postscript

Tubular legs, the reader will say, must be lighter than solid ones. True; but they will also be fatter. So it depends on the relative importance Snr. Tavolino attaches to his two design criteria — lightness and slenderness — and only he can decide that. If he can be persuaded to live with larger diameter legs, tubing can be considered — and the material choice may be different. Materials selection when section-shape is a variable appears in later Case Studies.

Ceramic legs were eliminated because of low toughness. If (improbably) the goal was to design a light, slender-legged table for use at high temperatures, ceramics should be reconsidered. The brittleness problem can be circumvented by more sophisticated design: by protecting the legs from abuse, or by prestressing them in compression.

Further Reading

Young, WC (1989), 'Roark's Formulas for Stress and Strain', 6th edition, McGraw-Hill, NY

Related Case Studies

1. Materials for Oars

2. Mirrors for Large Telescopes