Materials For Oars

• Introduction
• The model
• Selection
• Postscript
• Further reading
• Related case studies

Introduction

Credit for inventing the rowed boat seems to belong to the Egyptians. Boats with oars appear in carved relief on monuments built in Egypt between 3300 and 3000BCE. Boats, before steam power, could be propelled by poling, by sail and by oar. Oars gave more control than the other two, and their military potential was well understood by the Romans, the Vikings and the Venetians.

Records of rowing races on the Thames in London extend back to 1716. Originally the competitors were watermen, rowing the ferries which carried people and goods across the river. Gradually gentleman became involved (notably the young gentlemen of Oxford and Cambridge), sophisticating both the rules and the equipment. The real stimulus for development of high performance boats and oars came in 1900 with the establishment of rowing as an Olympic sport. Since then both have exploited to the full the craftsmanship and materials of their day. Consider, as an example, the oar (Figure 2-1). The requirements of the design are summarized in Table 2-1.

Figure 2-1. Oars are designed on stiffness, measured in the way shown in the lower figure; and they must be light

Table 2-1. The design requirements

The Model

Mechanically speaking, an oar is a beam, loaded in bending. It must be strong enough to carry the bending moment exerted by the oarsman without breaking, it must have just the right stiffness to match the rower's own characteristics and give the right 'feel', and — very important — it must be as light as possible. Meeting the strength constraint is easy. Oars are designed on stiffness, that is, to give a specified elastic deflection under a given load. The upper part of Figure 2-1 shows an oar: a blade or 'spoon' is bonded to a shaft or 'loom' which carries a sleeve and collar to give positive location in the rowlock. The lower part of the figure shows how the oar stiffness is measured: a 10 kg weight is hung on the oar 2.05 m from the collar and the deflection at this point is measured. A soft oar will deflect nearly 50 mm; a hard one only 30 mm. A rower, ordering an oar, specifies how hard it should be.

The oar must also be light; extra weight increases the wetted area of the hull and the drag that goes with it. So there we have it: an oar is a beam of specified stiffness and minimum weight.

The mass, m, of the oar — treated as a solid cylinder — is

(M2.1)

where A is the area of the cross-section and ρ the density of the material of which it is made. This is the objective function — the quantity to be minimized. The stiffness of the beam is

(M2.2)

where E is the modulus, I is the second moment of area of the beam and C is a constant (roughly 24 — the material selection is independent of its value). For a solid cylinder

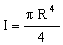(M2.3)

The length L and stiffness S are specified: they are constraints. The free variable is the radius R. We use equations (M2.2) and (M2.3) to eliminate R in equation (M2.1) giving

(M2.4)

The mass m of the oar is minimized by choosing materials with large values of

(M2.5)

The design requirements list two further constraints — on toughness G_c and cost C_m. These are frequently taken for granted — the designer subconsciously rejects materials which are too brittle (glass, for instance) or too costly (platinum). It is better to make them explicit. We therefore require that the limits set out in Table 2-1 are met.

The Selection

The selection has two stages. Figure 2-2 shows the first. It is a chart of Young's modulus, E, against density, ρ. A selection line for the index is shown on it. It identifies three classes of material: woods, carbon- and glass-fiber reinforced polymers and certain ceramics (Table 2-2). Ceramics meet the first set of design requirements, but are brittle; a ceramic oar, if dropped, might shatter.

Shock-resistance requires adequate toughness, G_c, (not just fracture toughness, K_1c). A useful rule-of-thumb for this is to chose materials with a toughness, G_c, such that

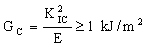(M2.6)

We require a second stage as shown in Figure 2-3: a chart of toughness against cost. The toughness axis is created by generating a user-defined property combination with K_1c and E, as per equation M2.6. A box selection specifies materials with

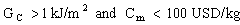
Ceramics are eliminated because they are brittle. The recommendation is clear. Make your oars out of wood or — better — out of CFRP.

Figure 2-2. A chart of modulus, E, against density, ρ. The selection line is placed at M₁ = 0.006 GPa^1/2/(kg/m³).

Table 2-2. Materials for oars

Figure 2-3. A chart of toughness, G_c, against cost/kg, C_m. The box isolates materials with G_c  > 1 kJ/m² and C_m  < 100 USD/kg (75 GBP/kg).

Postscript

Now we know what oars should be made of. What, in reality, is used? Racing oars and sculls are made of wood or of a high performance composite: carbon-fiber reinforced epoxy, CFRP.

Wooden oars are made today, as they were 100 years ago, by craftsmen working largely by hand. The shaft and blade are of Sitka spruce from the northern US or Canada, the further north the better because the short growing season gives a finer grain. The wood is cut into strips, four of which are laminated together to average the stiffness. A strip of hardwood is bonded to the compression-side of the shaft to add stiffness, and the blade is glued to the shaft. The rough oar is then shelved for some weeks to settle down, and then finished by hand cutting and polishing. The final spruce oar weighs between 4 and 4.3 kg, and costs (in 1994) about £150 ($250).

Composite blades are a little lighter than wood, for the same stiffness. The component parts are fabricated from a mixture of carbon and glass fibers in an epoxy matrix, assembled and glued. The advantage of composites lies partly in the saving of weight (typical weight: 3.9 kg) and partly in the greater control of performance: the shaft is molded to give the stiffness specified by the purchaser. At a price, of course: a CFRP oar costs about £300 ($450).

Could we do better? The Chart shows that wood and CFRP offer the lightest oars, at least when normal construction methods are used. Novel composites, not at present shown on the chart, might permit further weight saving; and functional-grading (a thin, very stiff outer shell with a low density core) might do it. But both appear, at present, unlikely.

Further Reading

Redgrave, S, 'Complete Book of Rowing', (1992), Partridge Press, London.

Related Case Studies

1. Mirrors for Large Telescopes

2. Materials for Table Legs