Mirrors For Large Telescopes

• Introduction
• The Model
• The Selection
• Postscript
• Further reading
• Related case studies

Introduction

The world's largest single-mirror optical telescope is sited on Mount Semivodrike, near Zelenchukskaya in the Caucasus Mountains of Russia in the USSR. The mirror is 6 m (236 inches) in diameter, but it has never worked very well. The largest satisfactory single-mirror reflector is that at Mount Palomar in California; it is 5.08 m (200 inches) in diameter. To be sufficiently rigid, the mirror, which is made of glass, is nearly 1 m thick and weighs 70 tonnes. Other, larger, telescopes exist or are planned, but the cost has proved to be an obstacle. ⁵

The total cost of a large (220-inch) telescope is, like the telescope itself, astronomical — about US $280m. The mirror itself accounts for only about 5% of this cost; the rest is that of the mechanism which holds, positions and moves it as it tracks across the sky. This mechanism must be stiff enough to position the mirror relative to the collecting system with a precision, d, about equal to that of the wavelength of light. It might seem, at first sight, that doubling the mass m of the mirror would require that the sections of the support-structure be doubled too, so as to keep the stresses (and hence the strains and displacements) the same; but the heavier structure then deflects under its own weight. In practice, the sections have to increase as m², and so does the cost.

Before the turn of the century, mirrors were made of speculum metal, a copper-tin alloy. The Earl of Rosse (1800-1867), who lived in Ireland, had one; he discovered spiral galaxies with it. But the biggest speculum mirrors were never more than 1 m in diameter because of their enormous weight: the density of speculum is 8 Mg/m³. Since then, they have been made of glass (density: 2.3 Mg/m³), silvered on the front surface, so none of the optical properties of the glass are used. Glass is chosen for its mechanical properties only; the 70 tonnes of glass is just a very elaborate support for 100 nm (about 30g) of silver. Could one, by taking a radically new look at materials for mirrors, suggest possible routes to the construction of lighter, cheaper telescopes?

The design requirements are listed in Table 3-1.

Table 3-1. The design requirements

⁵ These include: the Keck telescope, a 10 m mirror on Mauna Kea, Hawaii made of 36 separate segments; the Very Large Telescope (VLT), four coupled 8 m mirrors on Cerro Paranal Silla, Chile; and the Large Binocular Telescope, two 8.4 m reflectors, on Mount Graham, Arizona, USA.

The Model

At its simplest, the mirror is a circular disk, of diameter 2R and mean thickness t, simply supported at its periphery (Figure 3.1). When horizontal, it will deflect under its own weight mg; when vertical it will not deflect significantly. This distortion (which changes the focal length and introduces aberrations into the mirror) must be sufficiently small that it does not interfere with performance. In practice, this means that the deflection δ of the midpoint of the mirror must be less than the wavelength of light. Additional requirements are: high dimensional stability (no creep), low thermal expansion, and immunity to changes in humidity.

Figure 3-1. The mirror of a large optical telescope is modeled as a disk, simply supported at its periphery. It must not sag by more than a wavelength of light at its center.

The mass of the mirror (the property we wish to minimize) is

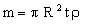(M3.1)

where r is the density of the material of the disk. The elastic deflection, δ, of the center of a horizontal disk simply supported at its edges, due to its own weight, for a material with Poisson's ratio of 0.3, is

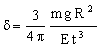(M3.2)

The quantity g in this equation is the acceleration due to gravity: 9.81 m/s². E, as before, is Young's modulus. We require that this deflection be less than (say) 0.1 mm. The diameter of the disk is specified by the telescope design, but the thickness is a free variable. Solving for t and substituting this into equation (M3.1) gives

(M3.3)

The lightest mirror is therefore the one with the greatest value of the performance index

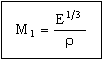(M3.4)

A second constraint is that of dimensional stability. Low thermal expansion, α, and high thermal conductivity, λ, help here because these control the thermal distortion of the mirror when it is heated or cooled. Thermal distortion is analyzed in detail in Minimizing Distortion in Precision Devices, where it is shown that the materials which distort the least are those with high values of

(M3.5)

The Selection

This is another example of elastic design for minimum weight. The appropriate chart is that relating Young's modulus E and density ρ (Figure 3.2). The selection-line has a slope of 3, corresponding to the condition

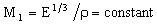Figure 3-2. The E-ρ chart. The diagonal line shows the index M₁ = 0.0017. Glass is better than most metals, among which beryllium is the best choice. Carbon-fiber reinforced polymers give, potentially, the lowest weight of all, but may lack adequate dimensional stability. Foamed or honeycomb-structured glass is an attractive candidate.

Glass lies on the line M₁ = 0.0017 (in the units of Figure 3-2). Materials which lie above it are better than glass, those below are worse. Glass is much better than steel or speculum metal (that is why most mirrors are made of glass); but it is less good than magnesium, beryllium, several ceramics, carbon-fiber and glass-fiber reinforced polymers, and — an unexpected finding — stiff foamed polymers.

This short list must now be screened for dimensional stability. The second stage, shown in Figure 3-3, displays the thermal conductivity λ and thermal expansion coefficient α of materials. The line of slope 1, corresponding to the condition

identifies materials with high M₂. Potential candidates are compared with glass in Table 3-2.

Figure 3-3. A chart of thermal conductivity, λ, against thermal expansion, α. The diagonal line shows one possible selection using the M₂ index.

One must, of course, examine other aspects of this choice. The mass of the mirror can be calculated from equation (M3.3) for the materials listed in the table. Note that the polystyrene foam, the CFRP and the beryllium mirrors are as much as one fifth the weight of the glass one, and that the support-structure could thus be as much as 25 times less expensive than that for an orthodox glass mirror. But could they be made?

Some of the choices — the polystyrene foam or the CFRP — may at first seem impractical. But the potential cost-saving (the factor of 25) is so vast that they are worth scrutiny. The most obvious obstacle is the poor thermal distortion characteristics and lack of stability of polymers. They change dimensions with age, humidity, temperature and even small stresses. But glass itself can be foamed to give a material with a density not much greater than polystyrene foam; or it can be stiffened by incorporating carbon fibers in it: both increase M₁. Both foamed and carbon-reinforced glass have the same chemical and environmental stability as solid glass. They could provide a route to large cheap mirrors.

Table 3-2. Mirror backing for 200-inch telescope

Postscript

There are, of course, other things you can do. The stringent design criterion (δ < 10 μm) can be partially overcome by engineering design without reference to the material used. The mirror can, for instance, be supported by small hydraulic jacks that exert distributed forces over its back surface, controlled to vary automatically with the attitude of the mirror. But the limitations of this sort of mechanical system still require that the mirror meets a stiffness-target. While stiffness at minimum weight is the design requirement, the criteria for material-selection remain unchanged.

Radio telescopes do not have to be as precisely dimensioned as optical ones because they detect radiation with a longer wavelength. But they are much bigger (60 meters rather than 6). They suffer from the same problems of distortion caused by self-weight. Microwaves have wavelengths in the mm band, requiring precision over the mirror face of 0.25 mm. A recent 45 m radio telescope built for the University of Tokyo achieves this, using CFRP reflector. Its parabolic surface is made of 6000 CFRP panels, each servo controlled to compensate for macro-distortion.

Beryllium appears on our list. It is light, stiff, and has a low coefficient of thermal expansion. Small mirrors for space applications must be light for a different reason (to reduce take-off weight) and must, in addition, be as immune as possible to temperature change. Here beryllium comes into its own.

Further Reading

Clement, TF, Parsonage, TB and Kuxhaus, MB. 'Advanced Materials and Processes', (1992), 3/92, pp. 37–40.

Related Case Studies

1. Materials for Oars

2. Materials for Table Legs

3. Minimizing Distortion in Precision Devices