
Middle-aged readers may remember expensive watches with the words "17 Sapphires" printed on the face, roughly where the word "Quartz" now appears. The message was that the mechanism had bearings made of sapphire (Al2O3) and that that was good. A really expensive watch had, not sapphires, but diamonds.
They are examples of good materials for knife edges and pivots. These are bearings in which two members are loaded together in nominal line or point contact, and can tilt relative to one another, or rotate freely about the load axis (Figure 13.1). The main requirements of materials for such bearings are high hardness (to carry the contact pressures) and high modulus (to give positional precision and to minimize frictional losses). But in what combination? The answer depends on the objective: maximum precision or maximum load-capacity. Table 13.1 summarizes the requirements.

Figure 13.1 A knife edge and a pivot. They have small contact area, for precision, and high strength, to avoid damage by contact stresses.
|
FUNCTION |
Knife edges and pivots |
|
OBJECTIVE |
(a) Maximize positional precision for given load |
|
(b) Maximize load capacity for given geometry |
|
|
CONSTRAINTS |
(a) Contact stress must not cause damage to either surface |
|
(b) Adequate toughness (for pivots exposed to shock loading) |
|
|
(c) Low thermal expansion (for high precision pivots) |
Table 13.1 The design requirements
Consider maximizing precision first. The positional accuracy of a pivot or knife edge increases, and its frictional losses decrease as the area of contact A is made smaller and smaller. To maximize precision, we seek to minimize A, but as we do so, the contact pressure rises. For a given load, F, the peak contact pressure p is given by Herzian contact theory; it is:
 |
(M13.1) |
If both surfaces are to remain elastic, this pressure must not exceed their hardness, H, divided by a safety factor, which we ignore. (It does not affect the outcome of the analysis.) Thus
 |
(M13.2) |
Thus the area of contact is minimized, and the precision maximized, by selecting materials with large values of the performance index
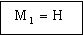 |
(M13.3) |
Now consider the alternative objective: that of maximizing the load that the pivot can support at fixed geometry. Herzian contact theory gives the maximum pressure in the contact zone of a hemispherical pivot-tip pressed against a flat block by a force F as
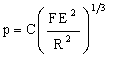 |
(M13.4) |
where R is the radius of curvature of the tip of the pivot, E is its elastic modulus and C is a constant close to unity. The constraint remains the same: this pressure must not exceed the hardness H of the pivot or the block. Thus
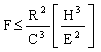 |
(M13.5) |
The load is maximized, for a given geometry R, by choosing materials with large values of the performance index
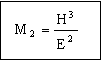 |
(M13.6) |
The performance indices involve H and E. Figure 13.2 shows the appropriate chart. For precision you want high M1, and then ceramics are definitely the best choice: Al2O3 (sapphire), silicon carbide and nitride, and — above all — diamond. Cermets (composites of tungsten carbide and cobalt) are the only other class of solid which competes with them. For load-bearing capacity, you want high M2 instead; then high-carbon steels, tool steels and high-strength titanium alloys become possibilities, although ceramics and cermets remain the most attractive candidates.

Figure 13.2(a) Chart of hardness H against modulus E, showing the index M1.

Figure 13.2(b) Chart of hardness H against modulus E, showing the index M2.
But there is more to it than that. Change of temperature will influence the positional accuracy of a pivot. Precision is maintained by choosing materials with low thermal expansion. Robustness, on the other hand, requires that the pivot or knife-edge survive rough handling — and for this a degree of toughness is desirable. Figure 13.3 shows a chart of fracture toughness plotted against thermal expansion coefficient. Using this as a second stage, gives the selections in Tables 13.2(a) and (b).

Figure 13.3 A chart of fracture toughness, K1c, against thermal expansion coefficient, λ, showing the selection stage for robust, precise, pivots.
|
MATERIAL |
 |
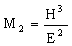 |
COMMENT |
|
(GPa) |
(MPa) |
||
|
Diamond |
8000 |
0.2 |
Outstanding on all counts except cost. |
|
Tungsten Carbide, WC |
4000 |
0.1 |
Excellent M1 and M2, good corrosion resistance, poor K1c |
|
Silicon Carbide, SiC |
3000 |
0.1 |
Excellent M1 and M2, good corrosion resistance, poor K1c |
|
Silicon Nitride, Si3N4 |
2200 |
0.11 |
Excellent M1 and M2, good corrosion resistance, poor K1c |
|
Zirconium Carbide, ZrC |
|
|
Excellent M1 and M2, good corrosion resistance, poor K1c |
|
Sapphire, Al2O3 |
2000 |
0.09 |
Good M1 and M2, good corrosion resistance, poor K1c |
|
Glass and Silica |
1000 |
0.05 |
Good M1 but brittle — poor K1c |
|
High-Carbon Steel |
400 |
0.02 |
Good M1 and M2, poor corrosion resistance, but excellent K1c |
Table 13.2(a) Materials for precise knife edges and pivots
|
MATERIAL |
 |
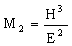 |
COMMENT |
|
(GPa) |
(MPa) |
||
|
High-Carbon Steel |
400 |
0.02 |
Good M1 and M2, poor corrosion resistance, but excellent K1c |
|
Cermets |
500 |
0.03 |
Better than steel on all counts except cost |
|
Silicon Carbide, SiC |
3000 |
0.1 |
Excellent M1 and M2, good corrosion resistance, poor K1c |
|
Silicon Nitride, Si3N4 |
2200 |
0.11 |
Excellent M1 and M2, good corrosion resistance, poor K1c |
|
Diamond |
8000 |
0.2 |
Outstanding on all counts except cost and toughness |
Table 13.2(b) Materials for robust knife edges and pivots
The final choice depends on the details of its application. In sensitive force balances and other measuring equipment, very low friction is important: then we need the exceptionally high modulus of sapphire or diamond. In high load-capacity devices (weighbridges, mechanical testing equipment), some ability to absorb overloads by limited plasticity is an advantage, and hardened steel is a good choice. If the environment is a potentially corrosive one — and this includes ordinary damp air — glass or a ceramic may be best.
'Tribology Handbook' (1973) Ed. Neale, MJ, Butterworths, London, Section C6.
'Elsevier Materials Selector' (1991) Eds. Waterman, NA and Ashby, MF, Elsevier, Amsterdam, Section 1.5.3, p. 358 et seq.