.jpg)
Nature makes much use of elastic hinges: skin, muscle, cartilage all allow large, recoverable deflections. Man, too, designs with flexural hinges and elastic couplings: devices which connect or transmit load between components while allowing limited relative movement between them by deflecting elastically (Figure 10.1). Which materials are good for this?
The design requirements depend on the application. If the hinge carries no (or very little) axial load, then the objective is to maximize its movement, that is, the curvature to which it can be bent without damage (Table 10.1, Option (a)). But if it also carries axial loads, these impose a further constraint and the requirements change (Option (b)).
.jpg)
Figure 10.1 An elastic or 'flexure' hinge. The ligaments must bend repeatedly without failing.
FUNCTION |
Elastic hinge (possibly with axial load) |
OBJECTIVE |
Maximize elastic flexure or twisting |
CONSTRAINTS |
Must not fail by yield, sy; flexure, sMOR; fatigue, se; or fracture, sfr. |
(a) No axial load |
|
(b) With axial load |
Table 10.1 The design requirements
Consider the hinge for the lid of a box. The box, lid and hinge are to be molded in one operation. The hinge is a thin ligament of material which flexes elastically as the box is closed, as in Figure M10.1(a), but it carries no significant axial loads. Then the best material is the one which (for given ligament dimensions) bends to the smallest radius R without fracturing or failing by fatigue.
When a ligament of thickness t is bent elastically to a radius R, the surface strain is
 , , |
(M10.1) |
and — since the hinge is elastic — the maximum stress is
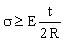 . . |
(M10.2) |
This stress must not exceed the modulus of rupture, σMOR, or the endurance limit σe, or the fracture strength σfr, whichever is least. We shall use the symbol σf to represent the failure stress, by which we mean the least of σy, σMOR, σe and σfr. Then the radius to which the ligament can be bend without damage is
 . . |
(M10.3) |
The best material is the one that can be bent to the smallest radius, that is, the one with the greatest value of the index
 . . |
(M10.4) |
We have assumed thus far that the hinge-thickness, t, is dictated by the way the hinge is made. But in normal use, the hinge may also carry repeated axial (tensile) forces, F, due to handling or due to the weight of the box and its contents. This sets a minimum value for the thickness, t, which is found by requiring that the tensile stress, F/tw (where w is the hinge-width) does not exceed the strength limit σf :
 |
Substituting this value of t into equation (M10.3) gives
 . . |
(M10.5) |
and the second index
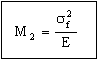 . . |
(M10.6) |
Both criteria involve ratios of σf and E. By way of example, we identify σf with the modulus of rupture, σMOR. We therefore create a chart of σMOR plotted against E (Figure 10.2). Candidates for unstressed hinges are identified by plotting M1 as a line of slope 1; it is shown at the position M1 = σf / E = 0.03. The best choices for the hinge are all polymers. The short list (Table 10.2) includes polyethylenes, polypropylene, nylon and, best of all, elastomers; these may be too flexible for the body of the box, but are good for the coupling. Cheap products with this sort of elastic hinge are generally molded from polyethylene, polypropylene or nylon. Spring steel and other metallic spring materials (like phosphor bronze) are less good by the criterion M1.

Figure 10.2(a) A chart of endurance limit σe against modulus E, enabling selection of materials with large values of M1.

Figure 10.2(b) A chart of endurance limit σe against modulus E, enabling selection of materials with large values of M2.

Figure 10.3(a) The same chart as Figure 10.2(a), showing M1, using the Polymers record subset

Figure 10.3(b) The same chart as Figure 10.2(b), showing M2, using the Polymers record subset
Steel, bronze and beryllium-copper come into their own when axial loads exist. Figure 10.2(b) shows M2, positioned at M2 = 5; the metals are now better than the polymers.
Which index should we now use? It depends on the magnitude of F. When F is very small, the hinge thickness required to carry it is less than that (t*) set by processing; then the first index, M1, is the one we want. When F is large, it is M2. The coupling between them — the intersection of the M1-M2 grids — is found by equating the two equations for R, (equations (M10.3) and (M10.5)), using the process-limited minimum value of the thickness t*, in equation (M10.3). This gives what we call the coupling equation:
 |
Specified F, t* and w (determined by the box dimensions) give a value for σf* at which the indices M1 and M2 intersect; the best choice of material is that which lies along both lines. So, for small F, the original index was the right one; only for large F do we switch to the second.
MATERIAL |
M1 (x 10-3) |
M2 (MJ/m3) |
COMMENT |
Polyethylenes |
30 – 45 |
1.6 – 1.8 |
Widely used for cheap hinged bottle caps, etc |
Polypropylene |
30 |
1.6 – 1.7 |
Stiffer than PEs. Easily molded |
Nylon |
30 |
2 – 2.1 |
Stiffer than PEs. Easily molded |
PTFE |
35 |
2 – 2.1 |
Very durable; more expensive than PE, PP, etc. |
Elastomers |
100 – 300 |
10 – 20 |
Outstanding, but low modulus |
Beryllium-copper |
5 – 10 |
8 – 12 |
M1 less good than polymers. Use when high stiffness required |
Spring steel |
5 – 10 |
10 – 20 |
M1 less good than polymers. Use when high stiffness required |
Table 10.2 Materials for elastic hinges
Polymers give more design-freedom than metals. The elastic hinge is one example of this, reducing the box, hinge and lid (3 components plus the fasteners needed to join them) to a single box-hinge-lid, molded in one operation. The elastomeric coupling — a flexible universal joint (Figure M10.1), is another: it allows high angular, parallel and axial flexibility with good shock absorption characteristics and low cost. When axial loads are small, polymers are the best choice; but when axial loads become large, metals are better — they combine usable σe/E with high E, giving flexibility with good positional stability (as in the suspensions of relays).
'Tribology Handbook' (1973) Ed. Neale, MJ, Butterworths, London, Section C6.
'Elsevier Materials Selector' (1991) Eds. Waterman, NA and Ashby, MF, Elsevier, Amsterdam, Section 1.5.3, p. 388 et seq.