.jpg)
Springs come in many shapes and have many purposes. One thinks of axial springs (a rubber band, for example), leaf springs, helical springs, spiral springs, torsion bars and so on (Figure 9.1). Regardless of their shape or use, the best material for a spring is that which can store the greatest elastic potential energy per unit mass (or volume), without failing. The performance indices derived below, can be used to identify materials which satisfy the design specification summarized in Table 9.1.
.jpg)
Figure 9.1 Springs have many shapes, but all perform the same function: that of storing elastic energy.
FUNCTION |
Elastic Spring |
OBJECTIVE |
(a) Maximum stored elastic energy/unit volume |
(b) Maximum stored elastic energy/unit mass |
|
CONSTRAINTS |
No failure by yield, fatigue or fracture (whichever is more restrictive) |
Adequate toughness (Gc > 1 kJ/m2) |
|
Reasonable cost per unit weight (Cm < 100 GBP/kg) |
Table 9.1 The design requirements
The primary function of a spring is that of storing elastic energy and releasing it again when required. The elastic energy stored per unit volume in a block of material stressed uniformly to a stress σ is:
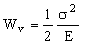 , , |
(M9.1) |
where E is the Young's modulus. It is this that we wish to maximize. The spring will be damaged if the stress σ exceeds the yield stress or failure stress σf. So the constraint is σ ≤ σf. The maximum energy density is therefore:
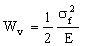 , , |
(M9.2) |
Torsion bars and leaf springs are less efficient than axial springs because some of the material is not fully loaded: the material at the neutral axis, for instance, is not loaded at all. For solid torsion bars 7
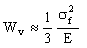 , , |
(M9.3) |
and for leaf springs loaded in pure bending the maximum energy storage is
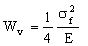 . . |
(M9.4) |
But, as these results show, this has no influence on the choice of material. The best material for springs, regardless of the way in which they are loaded, is that with the biggest value of
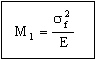 . . |
(M9.5) |
If mass matters rather than volume, we must divide this by the density ρ (giving energy stored per unit mass), and seek materials with high values of
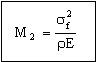 . . |
(M9.6) |
7 The value of the constant (1/3, 1/4) in equations (M9.3) and (M9.4) can be increased by prestressing: the maximum working stress of torsional and leaf springs is increased by straining the material beyond its elastic limit and then releasing the load.
The selection of materials for springs of minimum volume is shown in Figure 9.2. Here the modulus of rupture, σMOR, has been used as the measure of the failure strength σf. The chart shows σMOR plotted against modulus, E. A family of lines of slope 1/2 link materials with equal values of M1 = σf2/E. Those with the highest values of M1 lie towards the top left. The heavy line is one of the family. It is positioned at 10 MJ/m3 such that a small subset of materials is left exposed. They include high-strength steel (spring steel, in fact) lying near the top end of the line, and, at the other end, rubber. But certain other materials are suggested too: GFRP (now used for truck leaf springs), titanium alloys (good but expensive), glass fibers (used in galvanometers) and — among polymers — nylon (children's toys often have nylon springs). The procedure identifies a candidate from almost every material class: metals, glasses, polymers, elastomers and composites. A protective stage, limiting the values of the toughness Gc (Gc = K1c2 / E) and the cost Cm to the those listed in the design requirements, has been added (Figure 9.3). The selection results are shown in Table 9.2.
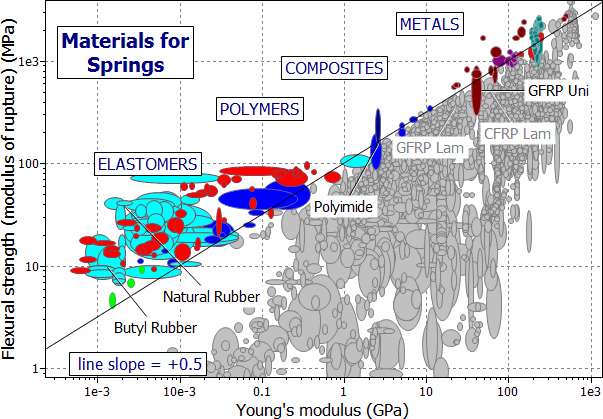
Figure 9.2 A chart of the modulus of rupture, σMOR, against Young's modulus, E. The diagonal line shows M1.
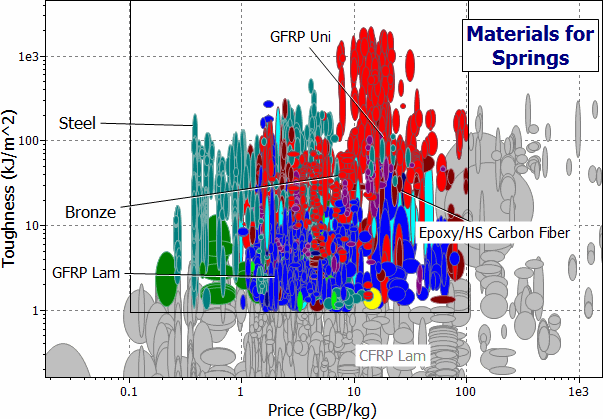
Figure 9.3 A 'protective' chart of the toughness, Gc, against cost per unit weight, Cm. The box restricts the selection to materials with Gc > 1 kJ/m2 and Cm < 100 GBP/kg.
MATERIAL |
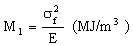 |
COMMENT |
Spring Steel |
15 – 25 |
The traditional choice: easily formed and heat treated. |
Ti Alloys |
15 – 20 |
Expensive, corrosion-resistant. |
CFRP |
15 – 20 |
Comparable in performance with steel; expensive. |
GFRP |
10 – 12 |
Almost as good as CFRP and much cheaper. |
Glass fibers |
30 – 60 |
Brittle in tension, but excellent if protected against damage; very low loss factor. |
Nylon |
1.5 – 2.5 |
The least good; cheap and easily shaped, but high loss factor. |
Rubber |
20 – 60 |
Better than spring steel; but high loss factor. |
Table 9.2 Materials for efficient springs of low volume
Materials selection for light springs is shown in Figure 9.4. It is a chart of σMOR/ρ against E/ρ, where ρ is the density. Lines of slope 1/2 now link materials with equal values of
|
One is shown at the value M2 = 2 kJ/kg. The new selection is listed in Table 9.3. Composites, because of their lower densities, are better than metals. Elastomers are better still (you can store almost 8 times more elastic energy per unit weight in a rubber band than in the best spring steel). Elastomeric springs are now widely used in aerospace because of their low weight and high reliability. Wood — the traditional material for archery bows, now appears in the list.
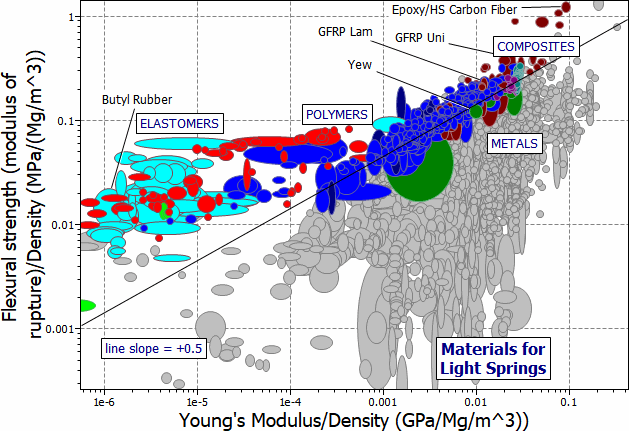
Figure 9.4 A chart of σMOR/ρ against E/ρ. The diagonal line is a contour of M2.
Many other considerations enter the choice of a material for a spring. Springs for vehicle suspensions must resist fatigue (the selection should then be made with the endurance limit, σe, replacing the modulus of rupture, σMOR). Valve springs for internal combustion engines must cope with elevated temperatures; here a strength-at-temperature is needed. The mechanical loss coefficient is important in springs which are loaded dynamically: polymers have high loss factors and therefore dissipate energy when they vibrate; metals, if strongly hardened, do not. Polymers, because they creep, are unsuitable for springs which carry a steady load, though they are good for catches and locating-springs which spend most of their time unstressed. Springs made from unprotected carbon-steel fail rapidly in a chemically corrosive environment. The least expensive solutions to this problem is to plate or polymer-coat them to provide a corrosion barrier, but if the coating is damaged, failure can follow. The more expensive solution is to make the spring from an intrinsically corrosion-resistant material: stainless steel, copper alloys, nickel and cobalt alloys, titanium alloys, reinforced polymers, GFRP or CFRP. If high thermal or electrical conduction is required, copper-beryllium alloys are the best choice. But these are secondary selection-criteria. The primary criterion, important in defining the initial subset of materials, remains that defined by equations (M9.5) and (M9.6).
MATERIAL |
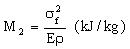 |
COMMENT |
Spring Steel |
2 – 3 |
Poor, because of high density. |
Ti Alloys |
2 – 3 |
Better than steel; corrosion-resistant; expensive. |
GFRP |
4 – 8 |
Better than steel; expensive. |
CFRP |
3 – 5 |
Better than steel; less expensive than CFRP. |
Glass fibers |
10 – 30 |
Brittle in torsion, but excellent if protected. |
Woods |
1 – 2 |
On a weight basis, wood makes good springs. |
Nylon |
1.5 – 2 |
As good as steel, but with a high loss factor. |
Rubber |
20 – 50 |
Outstanding; 10 times better than steel, but with high loss factor. |
Table 9.3 Materials for efficient light springs
Boiten, RG (1963) 'The Mechanics of Instrumentation', Proc. IMechE. vol 177, No. 10, 269–288.
Hayes, M (1990) 'Materials Update 23: Springs', "Engineering", May (1990), pp 42–43.